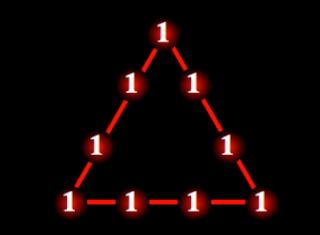
Esta problema es similar, en lugar de ser un cuadrado, será un triángulo (como el que aparece más abajo). En él se deberá colocar los números del 1 al 9, sin repetir, de tal manera que la suma de cada arista del triángulo sume una misma cantidad. Puesto que no es complicado, se plantea que se intente que, en primer lugar, la suma de las arista sea 20. Una vez superado este reto, podeis intentar que la suma de cada arista sea 17.
Suerte.
encontree el que sumaa 20 jaja:
ResponderEliminar6,1,9,4 ; 4,3,8,5 ; 5,7,8,6.
Ahora quiero mi punto en Topología jaja xD
WÓÓÓ! y el que suma 20!! =D
ResponderEliminar3,4,8,2 ; 2,5,9,1 ; 1,7,6,3.
Ahora si que exijo mi punto en Topología jajaj =)
Os doy mis soluciones:
ResponderEliminar-El que suma 17 creo si no me equivoco que es único,salvo giro de los vértices y permutación de los números centrales, y es como bien ha dicho divad el siguiente:
________1
______9___7
____5_______6
__2___8___4___3
-En cambio el que suma 20 no es único, podemos encotrar muchos que lo cumplen, como por ejemplo el que ha dicho divad o estos dos:
________4
______2___3
____9_______7
__5___8___1___6
________3
______4___9
____8_______1
__5___6___2___7
Añado una curiosidad, si no me equivoco, la menor suma que se puede formar en este triangulo es de 17 y la mayor suma es 23. Podeis realizar este último. Dicho esto último parece claro que la única forma de hacer el que suma 17 es colocando en los vértices los números 1,2 y 3.
Jajaja, muy buena José, estás en lo cierto, la suma máxima, tal y como dices, ha de ser 23 por arista.
ResponderEliminarExplicación: La suma de los 9 primeros naturales es 45. Pero tres de ellos serán los vértices, por lo que habrá 3 números que apareceran en dos aristas, lo máximo sería que esos números fuesen 7,8 y 9. Por lo que nos queda 45 + 24 = 69, entre 3 aristas del triángulo nos da 23 por arista =)
Razonamiento análogo para que la suma sea 17 por arista, en este caso los números de los vértices serían 1,2 y 3
:D
Jajaja, exacto, tal como yo lo había deducido :)
ResponderEliminarPD: Veo que este blog cada vez va cogiendo más vida jaja
PUTO
Eliminar:D ESTA SI ME SIRVIO PORQUE LO TENIAMOS QUE HACER EN LA ESCUELA PERO LA PROFA LO DEJO DE TAREA A POR CIERTO VOY EN 6° C DE PRIMARIA Y LLEGUE LUEGO LUEGO LO BUSQUE EN INTERNET Y AQUI ESTA LA RESPUESTA SE LA AGRADESCO A José Serrano Puerto GRACIAS ESTOY MUY AGRADECIDO BAY
ResponderEliminarNo hay hasta el1000 o 100 pro con triángulos más grandes
ResponderEliminar"No sabemos qué es, ni que forma tiene, ni siquiera si sirve para algo o no, pero lo hemos demostrado y es cierto."
ResponderEliminarsábado, 3 de diciembre de 2011
Problema: Triángulo mágico
Bueno, supongo que muchos de vosotros alguna vez habrá jugado a completar una especie de cuadrado "mágico" con ciertos números de tal manera que la suma de cada horizontal, vertical y diagonal sea la misma cantidad.
Esta problema es similar, en lugar de ser un cuadrado, será un triángulo (como el que aparece más abajo). En él se deberá colocar los números del 1 al 9, sin repetir, de tal manera que la suma de cada arista del triángulo sume una misma cantidad. Puesto que no es complicado, se plantea que se intente que, en primer lugar, la suma de las arista sea 20. Una vez superado este reto, podeis intentar que la suma de cada arista sea 17.
Suerte.
Publicado por Carlos Bejines en 19:33
Enviar por correo electrónico
Escribe un blog
Compartir con Twitter
Compartir con Facebook
Etiquetas: Problemas
8 comentarios:
Divad6 de diciembre de 2011 13:25
encontree el que sumaa 20 jaja:
6,1,9,4 ; 4,3,8,5 ; 5,7,8,6.
Ahora quiero mi punto en Topología jaja xD
Responder
Divad6 de diciembre de 2011 13:34
WÓÓÓ! y el que suma 20!! =D
3,4,8,2 ; 2,5,9,1 ; 1,7,6,3.
Ahora si que exijo mi punto en Topología jajaj =)
Responder
José Serrano Puerto6 de diciembre de 2011 18:14
Os doy mis soluciones:
-El que suma 17 creo si no me equivoco que es único,salvo giro de los vértices y permutación de los números centrales, y es como bien ha dicho divad el siguiente:
________1
______9___7
____5_______6
__2___8___4___3
-En cambio el que suma 20 no es único, podemos encotrar muchos que lo cumplen, como por ejemplo el que ha dicho divad o estos dos:
________4
______2___3
____9_______7
__5___8___1___6
________3
______4___9
____8_______1
__5___6___2___7
Añado una curiosidad, si no me equivoco, la menor suma que se puede formar en este triangulo es de 17 y la mayor suma es 23. Podeis realizar este último. Dicho esto último parece claro que la única forma de hacer el que suma 17 es colocando en los vértices los números 1,2 y 3.
Responder
C.Bejines6 de diciembre de 2011 18:27
Jajaja, muy buena José, estás en lo cierto, la suma máxima, tal y como dices, ha de ser 23 por arista.
Explicación: La suma de los 9 primeros naturales es 45. Pero tres de ellos serán los vértices, por lo que habrá 3 números que apareceran en dos aristas, lo máximo sería que esos números fuesen 7,8 y 9. Por lo que nos queda 45 + 24 = 69, entre 3 aristas del triángulo nos da 23 por arista =)
Razonamiento análogo para que la suma sea 17 por arista, en este caso los números de los vértices serían 1,2 y 3
:D
Responder
José Serrano Puerto6 de diciembre de 2011 19:10
Jajaja, exacto, tal como yo lo había deducido :)
PD: Veo que este blog cada vez va cogiendo más vida jaja
Responder
Respuestas
Anónimo4 de febrero de 2013 17:56
PUTO
Responder
Anónimo4 de febrero de 2013 17:55
:D ESTA SI ME SIRVIO PORQUE LO TENIAMOS QUE HACER EN LA ESCUELA PERO LA PROFA LO DEJO DE TAREA A POR CIERTO VOY EN 6° C DE PRIMARIA Y LLEGUE LUEGO LUEGO LO BUSQUE EN INTERNET Y AQUI ESTA LA RESPUESTA SE LA AGRADESCO A José Serrano Puerto GRACIAS ESTOY MUY AGRADECIDO BAY
Responder
Anónimo6 de mayo de 2013 21:51
No hay hasta el1000 o 100 pro con triángulos más grandes
Responder
Hola que tal me ayudar con un triangulo magico es igual al anterior sólo que este se llena con numeros del 0 al 8 sin repetirse y que cada lado valga =12
ResponderEliminaresta si me sirvio de mucho ahora les toca a los que no lo tienen que lo busquen en esta pagina porque esta muy buena
ResponderEliminarComo resolver el del 69
ResponderEliminar